In thinking about ways to diagram spintronic circuits, it is beginning to seem to me that not every electronic circuit can be easily made with spintronic components. Specifically, can every spintronic circuit be decomposed into series-parallel pieces? That’s not true for electronic circuits, even with pure resistor circuits. That is, in finding the effective resistance of a network, sometimes you need to do more linear algebra than just the series-parallel law.
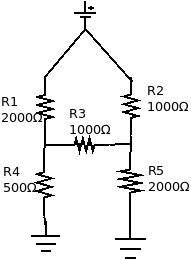
The simplest example is this one, where all edges have resistance 1 ohm except for the indicated edge which has a resistance of 2 ohms:

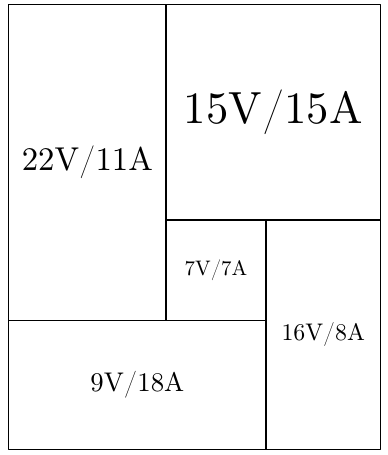
The effective resistance between the vertices marked “s” and “t” is 13/11, as elegantly proved with the following diagram:

Here each rectangle has width proportional to the current flowing through a corresponding resistor, and height proportional to the voltage difference. Thus the overall current is the overall width of 11, and the overall voltage difference is 13.
Is it possible to construct a spintronics circuit that mirrors the behaviour of that 5-resistor electronic circuit, with the effective resistance changing in the same way as the resistances vary? The first attempt I tried definitely did not work:
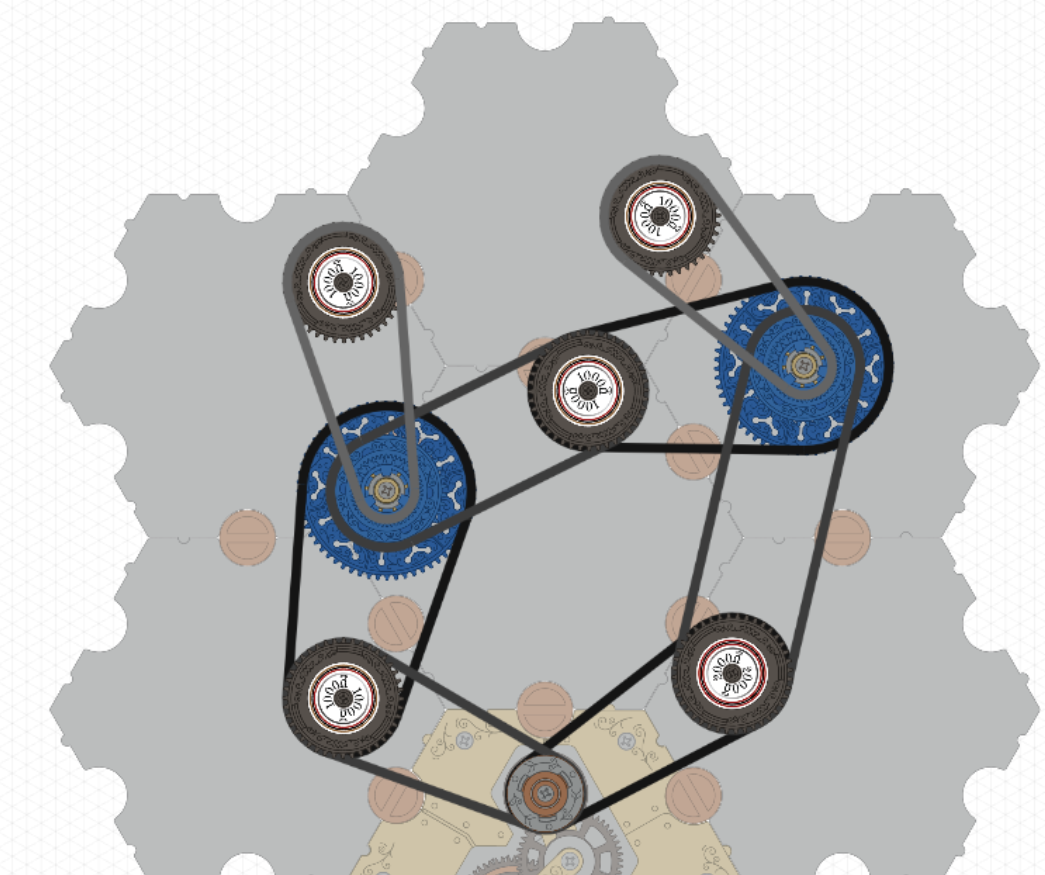
If you click on the link, you’ll see that one of the resistors (at the upper right) is rotating counterclockwise, which seems contrary to expectations.